이번 포스트(Part 1)에서는 TensorFlow로 DNN을 구현하기 전에 먼저 기본 개념을 알아보고 다음 포스트(Part 2)에서는 인공 신경망을 가능하게 한 Back Propagation 에 대해 알아보도록 하겠다.(모바일에는 최적화되어있지 않으니 가능하면 PC로 보시길 추천한다)
목차
Neural Network 역사
1943년, 워런 맥컬록(Warren McCulloch)와 월터 피츠(Walter Pitts)의 수학과 임계 논리(Threshold logic)라 불리는 알고리즘을 바탕으로 Neural Network 역사가 시작되었다.
하지만, 1969년에 마빈 민스키(Marvin Minsky)와 시모어 페퍼트(Seymour Papert)에 의해 기계학습 논문이 발표된 후 침체되었는데, 그 이유는 두 가지였다.
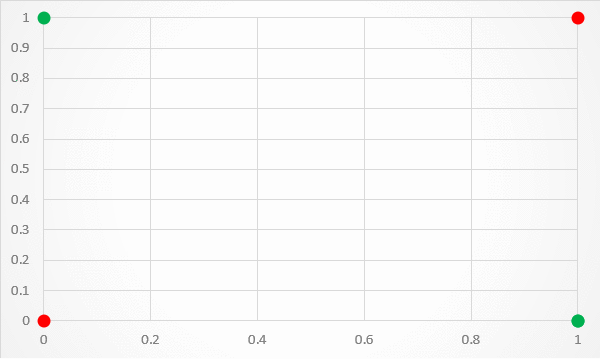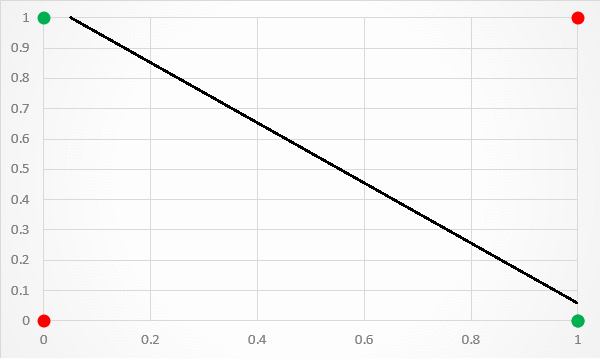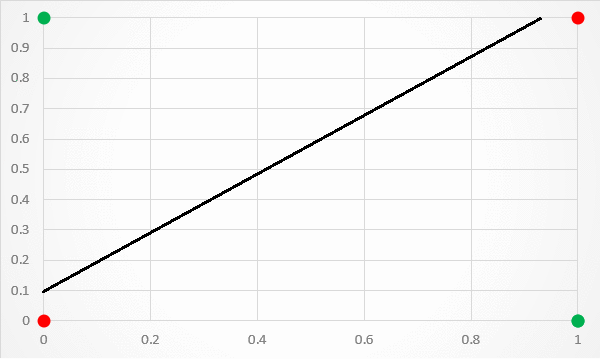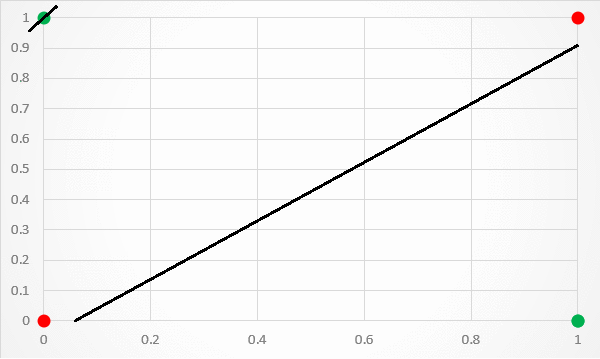
단층 신경망 은 선형으로 분류하기 때문에 아래의 그림처럼 문제가 배타적 논리합 회로(XOR problem)인 경우에는 해결하지 못한다.
Computing power가 부족하다.
위의 두 가지 문제점 외에도 가중치를 업데이트하기 위한 회로 수학 계산이 너무 복잡하였기에 오차역전파법(Back Propagation) 이 세상에 나오기 전까지는 연구가 침체될 수밖에 없었다.
Feedforward Propagation 설명
네트워크 초기화
$$
Input = \left[ \begin{array}{cccc}
i_{1} & i_{2} \\\end{array} \right]
$$
$$
W_{ij} = \left[ \begin{array}{cccc}
W_{i1j1} & W_{i1j2} & W_{i1j3} \\
W_{i2j1} & W_{i2j2} & W_{i2j3} \\\end{array} \right]
W_{jk} = \left[ \begin{array}{cccc}
W_{j1k1} & W_{j1k2} & W_{j1k3} \\
W_{j2k1} & W_{j2k2} & W_{j2k3} \\
W_{j3k1} & W_{j3k2} & W_{j3k3} \\ \end{array} \right]
W_{ko} = \left[ \begin{array}{cccc}
W_{k1o1} & W_{k1o2} \\
W_{k2o1} & W_{k2o2} \\
W_{k3o1} & W_{k3o2} \\ \end{array} \right]
$$
$$
Output = \left[ \begin{array}{cccc}
o_{1} & o_{2} \\\end{array} \right]
$$
이 포스트에서는 간단한 계산을 위해 Hidden layer가 2층 구조인 모형으로 초기화를 하였지만, 실제로는 layer마다 Neuron 개수나 Hidden layer의 층수는 우리가 알아내야 할 하이퍼 파라미터이다.
인공 신경망 알고리즘에는 여느 예측 문제와 마찬가지로 Feature에 해당하는 Input이 존재하고, 들어온 데이터들이 Hidden layer의 Neuron이 가진 하이퍼 파라미터에 의해 모양이 바뀌는 비선형 기저 함수
기저 함수 는 위에서 설명한 배타적 논리합 회로(XOR problem)를 해결하기 위한 방법으로, Input데이터 x대신 φ(x)를 사용하는 것을 의미한다. 여기서 "하이퍼 파라미터에 의해 모양이 바뀌는"라는 수식어가 붙은 이유는 Hidden layer로 이동할 때 계산되는 행렬(Matrix) 과 Bias 에 의해서 계속해서 모양을 바뀌는 것을 의미한다. 가장 기본적인 Activation 함수 인 Logistic Sigmoid를 예로 보자면, $$ Sigmoid = 1/(1+\mathrm{e}^{-(w_{ji}x + b_{j})}) $$ 형태의 기저함수를 가지게 되는 것.
에 의해서 비선형 문제를 해결할 수 있는 형태로 정보의 차원을 변경하며 전파하는 과정을 거친다. 마지막에는 Output으로 분류인 경우에는 Class 개수만큼, 회귀분석인 경우에는 1개의 실수값을 내보내는 것으로 마무리 된다.
역방향 전파(Back Propagation) 을 이해하기 위해서는 먼저 인공신경망의 계산 과정인 순방향 전파(Feedforward propagation) 를 이해해야 하므로 살펴보도록 하자.
Layer 1 (Input -> J)
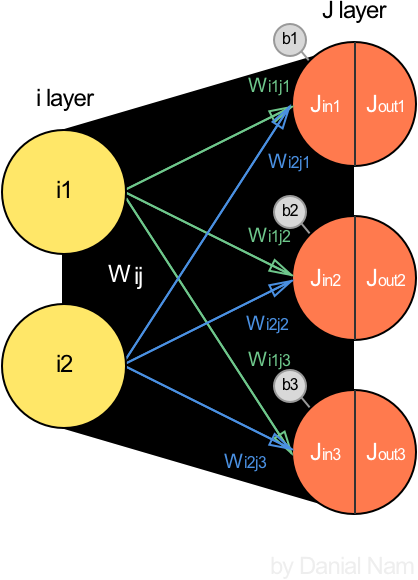
계산은 어려운게 없으니 따로 설명하지 않겠다. 중요한 점은 Hidden layer는 들어온 값(Jin)과 나가는 값(Jout)이 다르다는 것이다. 그 과정은 아래에서 살펴보자.
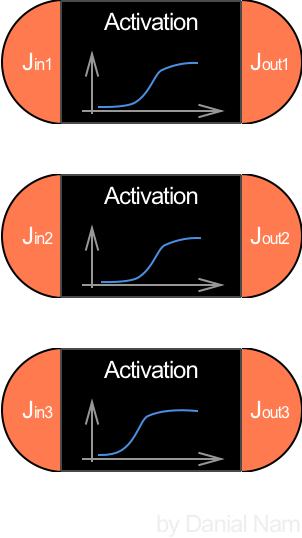
Hidden layer의 Neuron은 앞서 설명했듯 기저함수의 역할을 해야하므로 좌측의 그림처럼 Jin이 Activation function에 의해 변한 Jout을 다음 레이어에 들어가는 Input이 되게 한다. 이 포스팅의 예제에서 활성화 함수(Activation function) 은 모두 Logistic Sigmoid 함수를 사용하기로 한다.
$$ Sigmoid = 1/(1+\mathrm{e}^{-x}) $$ $$ Sigmoid(J_{in}) = \left[ \begin{array}{cccc} 1/(1+\mathrm{e}^{-J_{in1}}) \\ 1/(1+\mathrm{e}^{-J_{in2}}) \\ 1/(1+\mathrm{e}^{-J_{in3}}) \\\end{array} \right]^{T} = \left[ \begin{array}{cccc} J_{out1} \\ J_{out2} \\ J_{out3} \\\end{array} \right]^{T} $$이제는 위에서 설명한 하이퍼 파라미터에 의해 모양이 바뀌는이라는 표현이 이해가 더 잘 될 것이다. Jin은 wij와 bj에 의해 바뀌고 그에 의해 Jout이 바뀔 것이므로.
Layer 2 (J -> K)
Kin과 Kout 사이의 Activation function은 Layer 1에서와 마찬가지로 Logistic Sigmoid를 사용한다.
$$ Sigmoid(K_{in}) = \left[ \begin{array}{cccc} 1/(1+\mathrm{e}^{-K_{in1}}) \\ 1/(1+\mathrm{e}^{-K_{in2}}) \\ 1/(1+\mathrm{e}^{-K_{in3}}) \\\end{array} \right]^{T} = \left[ \begin{array}{cccc} K_{out1} \\ K_{out2} \\ K_{out3} \\\end{array} \right]^{T} $$Layer 1과 비교해서 새로운 점이 없으므로 그림상에 Notation은 자세하게 하지 않았다.
Layer 3 (K -> output)
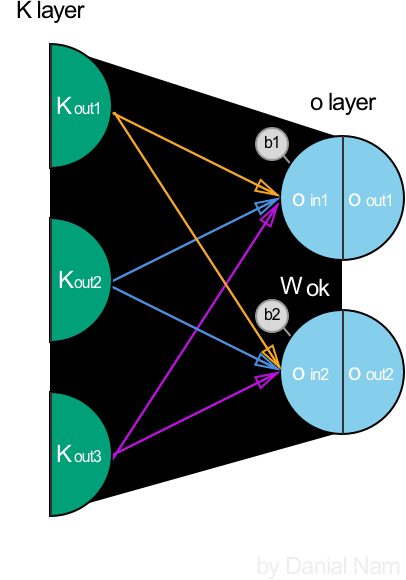
Output으로 나가는 값(oout)은 우리가 예측하고자하는 Target 값을 가장 잘 보여줄 수 있는 형태로 만들어야한다.
일반적으로는 회귀분석에는 특별한 활성화 함수 없이 내보내는 경우가 있지만, 만약 Target 데이터가 0보다 크고 1보다 작은 실수값만을 가진 상황이라면 Logistic Sigmoid을 사용했을 때 더 좋은 결과가 나올수도 있다는 의미다.
이 포스트에서는 분류 문제라고 가정하여 활성화 함수로는 Softmax를 이용하여 확률값처럼 변환시키는 것을 예로 들겠다.
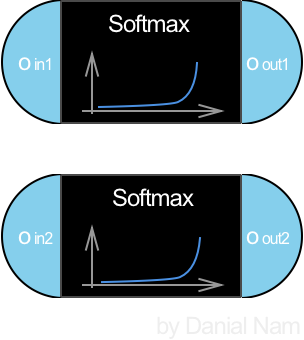
이렇게 Output으로 나온 oout 벡터가 우리의 예측값 y_pred이다. 물론 Random하게 초기화된 W, b값에 의해 예측한 값이라고 하기엔 터무니없는 값들이 나올 것임을 명심하자.
정리
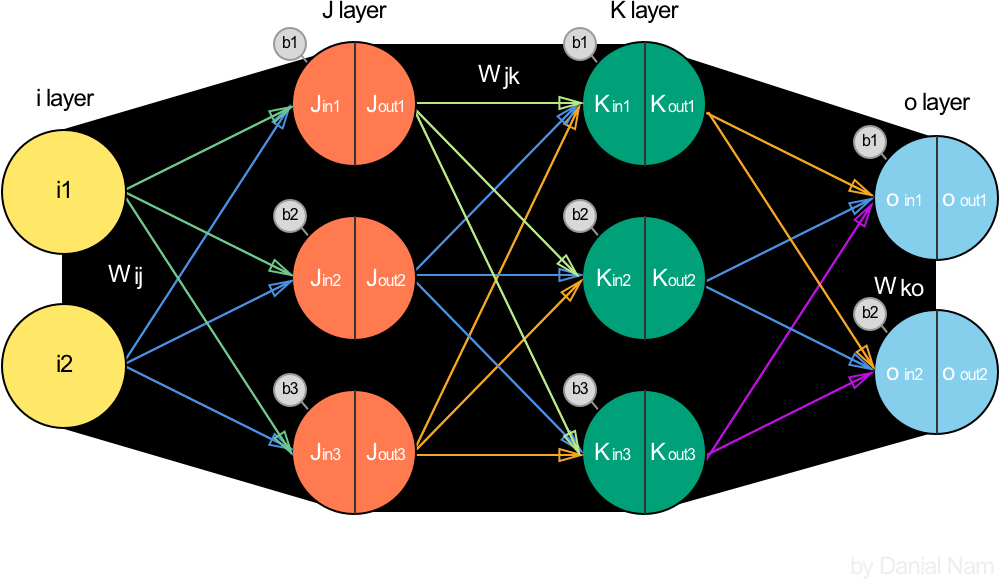
여기까지 계산 과정은 자세히 알아보았다. 현실 데이터들을 사용하게 되면 저것보다 Layer 개수나 각 Layer의 Neuron 개수는 차이가 나겠지만, 행렬 곱이란 점에서 식을 쓰는 법은 사실상 차이가 없을 것이다.
Neural network에 대해서 다시 생각해보자면 실제 인간 뇌의 "Neuron들이 input이 들어오면 어떤 임계값(Threshold)이상의 전기신호가 존재해야 전달하는 것"에서 아이디어를 얻은 것이므로,
위의 그림에서 J, K layer는 그런 Threshold가 넘는지를 활성화 함수(Activation function)을 통과시키며 해당 Neuron을 활성화할지 비활성화할지를 결정하는 과정인 것이다.
이제 고민해보자. input과 output은 우리가 측정한 실재하는 값이므로 변하지 않는 상수이지만, Hidden layer 내에서는 한 층을 통과할 때마다 새로운 값을 배출하고, 그 값을 다시 다음 층에서 받아서 또 통과시키면서 최초 input이 어떤 패턴을 가졌는지를 확인하는 과정이라고 볼 수 있지 않을까?
물론 패턴이라는 것은 해당 layer에서 활성화(우린 Sigmoid를 사용했으니, 0.5 이상인 경우를 활성화된 상태라고 하자)시킨 뉴런이 어떻게 분포해있는가를 말하는 것이고, 그 패턴을 해석한 파워는 input -> layer까지 오는 길에 계산한 W, b에서 나오는 것이므로, 이 값들을 우리는 더 정확한 패턴 해석을 위해서 학습하게 되는 것이다.
W, b가 우리의 학습하려는 값이라고 설명하면 끝나는 것을 길게 얘기했는데, 사실 필자도 이것이 어떻게 도움이 될지는 정확히 모르겠다. 하지만, 어떤 수학 문제가 있을 때 가장 쉽게 푸는 법을 알아내는 사람이 더 뛰어난 것이듯이,
분류 혹은 예측 성공률이 매우 높으면서도, 가장 적은 컴퓨팅 파워, 즉 해당 문제를 풀기 위한 가장 최적의 Layer 개수와 Neuron 개수가 존재할 수 있다는 것을 위의 해석 방식에서는 나타내고 있다는 점에서 의미가 있다고 본다.
이 분야를 공부하는 사람이라면 3Blue1Brown이라는 유튜버를 알고 있을 텐데, 그가 신경망이란 무엇인가? | 1장.딥러닝에 관하여에서 설명한 것에서 영감을 얻어 말로 풀어 설명한 것이니 영상을 보며 정리하면 더 도움이 될 것.
오차 함수(Cost function)
로지스틱 활성 함수를 이용한 분류 문제를 풀 때는 정답 y가 클래스 k에 속하는 데이터에 대해서 k번째 값만 1이고 나머지는 0인 one-hot-encoding 벡터를 사용한다.
Cost-function은 Cross-Entropy Error를 사용한다.
가중치 최적화
오차함수를 최소화하기 위해 아래처럼 미분(gradient)을 사용한 Steepest gradient descent 방법을 적용하자. 여기서 μ는 step size 혹은 learning rate라고 부른다.
문제점은 단순하게 수치적으로 미분을 계산하게되면 모든 가중치에 대해서 개별적으로 미분을 계산해야하는 문제가 있다. 하지만 역전파 (Back propagation) 을 사용하면 모든 가중치에 대한 미분값을 한번에 계산할 수 있다.
다음 포스트에서 자세하게 알아보도록 하자!
이번
인공신경망에 대한 이해 포스팅들은 시간을 많이 들여서 가능한 쉽고 직관적으로 설명하기 위해 노력하였다. 만약 도움이 되었다면! 공유를 부탁드린다!
Related Posts
Backpropagation calculus | Deep learning, chapter 4 by 3Blue1Brown
신경망 기초 이론
Danial Nam